The Challenge: From Particle Tracking to Data-Driven Turbulence Closure
Turbulent flows mix and transport scalars—temperature, species concentrations, pollutants—in complex ways that determine outcomes from combustion efficiency to atmospheric dispersion. Traditional Large Eddy Simulation (LES) approaches face a fundamental challenge: they must model the chemical source terms at subgrid scales, introducing uncertainties that compound in reacting flows. The closure problem becomes particularly acute when dealing with finite-rate chemistry, where small-scale fluctuations in composition and temperature dramatically affect reaction rates.
PICurv is being developed as a comprehensive Eulerian-Lagrangian framework with the long-term goal of enabling data-driven turbulence closure models. The project follows a staged development approach: first establishing robust particle tracking capabilities (current focus), then implementing scalar Filtered Density Function (FDF) methods, and ultimately developing joint velocity-scalar FDF approaches where machine learning can discover optimal closure strategies from high-fidelity data.
Currently, PICurv provides a foundation for particle-laden flow simulations and biomarker transport (such as platelet tracking in cardiovascular flows), while the infrastructure being built enables future FDF implementation.
Governing Equations: The LES Framework
In Large Eddy Simulation, we apply a spatial filter to the governing equations, resolving large-scale turbulent structures while modeling subgrid-scale (SGS) effects. For a passive or reacting scalar \(\phi\) (temperature, species mass fraction, etc.), the filtered transport equation is:
\[\frac{\partial \bar{\phi}}{\partial t} + \frac{\partial}{\partial x_j}(\tilde{u}_j \bar{\phi}) = \frac{\partial}{\partial x_j}\left(\Gamma \frac{\partial \bar{\phi}}{\partial x_j}\right) - \frac{\partial}{\partial x_j}(\tau_j^{\phi}) + \overline{S(\phi)}\] where:
- \(\bar{\phi}\) is the filtered scalar
- \(\tilde{u}_j\) is the filtered (Favre-averaged) velocity from the LES flow solver
- \(\Gamma\) is the molecular diffusivity
- \(\tau_j^{\phi} = \overline{u_j \phi} - \tilde{u}_j \bar{\phi}\) is the subgrid-scale scalar flux (requires modeling)
- \(\overline{S(\phi)}\) is the filtered chemical source term (requires modeling)
The Closure Problem
Two critical terms require closure models:
-
SGS Scalar Flux \(\tau_j^{\phi}\): Typically modeled using gradient diffusion assumptions (e.g., Smagorinsky-type models), but these are approximate and may not capture backscatter or complex SGS dynamics.
-
Filtered Source Term \(\overline{S(\phi)}\): For reacting flows with finite-rate chemistry, this is highly nonlinear. Standard approaches (assumed PDFs, flamelet models) impose restrictive assumptions about the SGS composition distribution.
The challenge: Both closures introduce modeling errors that accumulate and can dominate solution accuracy in complex flows.
The Filtered Density Function Approach
The FDF approach offers a fundamentally different perspective. Instead of tracking scalar means \(\bar{\phi}\), we track the filtered probability density function of scalar values at subgrid scales.
Definition
The scalar FDF is defined as:
\[\tilde{P}(\psi; \mathbf{x}, t) = \int G(\mathbf{x} - \mathbf{x}') \rho(\mathbf{x}') P(\psi; \mathbf{x}', t) d\mathbf{x}'\] where:
- \(\psi\) is the sample space variable for scalar \(\phi\)
- \(G\) is the LES filter kernel
- \(P(\psi; \mathbf{x}', t) = \delta(\psi - \phi(\mathbf{x}', t))\) is the fine-grained density
- \(\tilde{P}\) represents the filtered probability of finding scalar values in the range \([\psi, \psi + d\psi]\) within a filter volume
The key insight: if we know \(\tilde{P}\), we can compute any filtered scalar moment:
\[\bar{\phi} = \int \psi \tilde{P}(\psi) d\psi, \quad \overline{\phi^2} = \int \psi^2 \tilde{P}(\psi) d\psi, \quad \text{etc.}\] FDF Transport Equation
The FDF evolves according to:
\[\frac{\partial \tilde{P}}{\partial t} + \frac{\partial}{\partial x_j}(\tilde{u}_j \tilde{P}) = -\frac{\partial}{\partial \psi}[\langle S(\psi) | \psi \rangle \tilde{P}] - \frac{\partial}{\partial x_j}\langle u_j'' | \psi \rangle \tilde{P} + \frac{\partial}{\partial \psi}\left[\langle \frac{\partial}{\partial x_j}\left(\Gamma \frac{\partial \phi}{\partial x_j}\right) \Big| \psi \rangle \tilde{P}\right]\] | where $$\langle \cdot | \psi \rangle\(denotes conditional expectation given\)\phi = \psi$$. |
The crucial advantage: The chemical source term \(S(\psi)\) appears in closed form—no modeling assumptions needed! For any known chemical kinetics mechanism, we can evaluate \(S(\psi)\) exactly given composition \(\psi\).
Paradigm Shift: Traditional LES vs FDF-LES
| Aspect | Traditional LES | FDF-LES |
| Primary Variable | Filtered mean scalars \(\bar{\phi}\) | Filtered density function \(\tilde{P}(\psi)\) |
| SGS Scalar Flux | \(\tau_j^{\phi}\) requires closure (gradient diffusion, dynamic models) | \(\langle u_j'' | \psi \rangle \tilde{P}\) requires closure (mixing models) |
| Chemical Source Term | \(\overline{S(\phi)}\) requires closure (assumed PDFs, flamelet tables, conditional moment closure) | \(\langle S(\psi) | \psi \rangle \tilde{P}\) = \(S(\psi) \tilde{P}\) closed exactly |
| SGS Mixing | Implicitly handled through scalar diffusion model | Explicitly modeled (IEM, EMST, Curl) |
| PDF Information | Not directly available; requires assumptions | Full PDF available; all moments computed consistently |
| Computational Cost | Lower (Eulerian scalars only) | Higher (Lagrangian particles + Eulerian flow) |
| Advantages | Computationally efficient, well-established | Exact chemistry closure, unified statistics, no PDF assumptions |
| Challenges | Source term modeling errors accumulate | Requires particle management, mixing model uncertainties |
Key Insight: FDF-LES trades the chemical source term modeling problem for a transport/mixing modeling problem. Since chemistry is often more sensitive and complex than mixing, this is frequently a favorable trade-off, especially for combustion applications.
Why Lagrangian Particles?
While the FDF transport equation can theoretically be solved on an Eulerian mesh, this approach faces severe computational challenges:
The Grid-Lock Problem
While the FDF transport equation can theoretically be solved on an Eulerian mesh, this approach faces severe computational challenges:
| Challenge | Description | Impact |
| PDF Positivity | Standard discretization schemes can produce negative probability values | Non-physical results; violates fundamental PDF properties |
| Multiscale Chemistry | Composition space requires high resolution for many chemical species | Curse of dimensionality; computational cost scales exponentially with number of species |
| Numerical Diffusion | Eulerian advection schemes introduce artificial diffusion | PDF smearing; loss of sharp gradients in composition space |
| Mesh Resolution Mismatch | Physical space LES grid optimized for flow, not for composition statistics | Either under-resolve composition or waste resources with excessive physical grid refinement |
These issues make Eulerian FDF impractical for realistic problems, motivating the Lagrangian particle approach.
The Lagrangian Solution
Lagrangian particles provide an elegant alternative by solving equivalent stochastic differential equations (SDEs).
From Fokker-Planck to Langevin
The FDF transport equation is a Fokker-Planck equation in combined physical-composition space. By the Fokker-Planck ⇄ Langevin equivalence, we can solve an equivalent system of stochastic differential equations (SDEs) for particle trajectories.
For particle \(p\) with position \(\mathbf{X}^p(t)\) and composition \(\boldsymbol{\Phi}^p(t)\):
\[d\mathbf{X}^p = \tilde{\mathbf{u}}(\mathbf{X}^p, t) dt + \mathbf{B}(\mathbf{X}^p, t) d\mathbf{W}_x^p\] \[d\boldsymbol{\Phi}^p = \mathbf{S}(\boldsymbol{\Phi}^p) dt + \mathbf{M}(\boldsymbol{\Phi}^p, \mathbf{X}^p, t) dt\] where:
- \(\tilde{\mathbf{u}}\) is the filtered velocity field (from LES solver)
- \(\mathbf{B}\) represents SGS turbulent dispersion (requires modeling)
- \(\mathbf{W}_x^p\) is a Wiener process (Brownian motion)
- \(\mathbf{S}\) is the chemical source term (closed!)
- \(\mathbf{M}\) represents scalar mixing at subgrid scales (requires modeling)
In practice, these are advanced using operator splitting:
-
Physical space transport: Euler-Maruyama scheme for position update (drift + dispersion) \(\mathbf{X}^{p, n+1} = \mathbf{X}^{p, n} + \tilde{\mathbf{u}}(\mathbf{X}^{p, n}) \Delta t + \mathbf{B}(\mathbf{X}^{p, n}) \sqrt{\Delta t} \, \boldsymbol{\xi}^p\) where \(\boldsymbol{\xi}^p\) is a vector of random numbers from \(\mathcal{N}(0, 1)\)
-
Composition space evolution: Stiff ODE solver for chemistry + mixing \(\frac{d\boldsymbol{\Phi}^p}{dt} = \mathbf{S}(\boldsymbol{\Phi}^p) + \mathbf{M}(\boldsymbol{\Phi}^p, \langle \boldsymbol{\Phi} \rangle, \tau_{mix})\) Common mixing models include:
- IEM (Interaction by Exchange with the Mean): Relaxation toward local filtered mean
- EMST (Euclidean Minimum Spanning Tree): Pairwise mixing
- Curl: Modified Curl mixing model
Three Key Advantages
Key benefits of the Lagrangian particle method for FDF transport. [Image placeholder: Visual comparison of advantages]
- Zero Numerical Diffusion
- Particles carry scalar information exactly as they advect
- PDF sharpness naturally preserved without artificial smoothing
- No grid-induced smearing of composition distributions
- Unified Statistics
- Same particle ensemble yields all moments: \(\bar{\phi}\), \(\overline{\phi'^2}\), \(\overline{S(\phi)}\), full PDFs
- No need for separate scalar transport equations or assumed PDF shapes
- Consistency across all statistical quantities
- Simple Large-Timestep Chemistry
- Composition update is an ODE per particle (not PDE)
- Timestep not restricted by CFL in composition space
- Stiff chemistry solvers handle widely varying timescales naturally
- Vectorization/parallelization over particle ensembles
Development Strategy: Building the Foundation First
The FDF approach outlined above represents the project’s ultimate goal. However, implementing a production-quality FDF solver requires first establishing a robust foundation. The current development phase focuses on building and validating the core Eulerian-Lagrangian coupling infrastructure that will later support FDF transport.
Current Implementation: Newtonian Particle Tracking
PICurv currently implements massless tracer particles that follow the resolved Eulerian flow field. These particles solve the simplified transport equation:
\[\frac{d\mathbf{X}^p}{dt} = \tilde{\mathbf{u}}(\mathbf{X}^p, t) + \mathbf{u}_{SGS}(\mathbf{X}^p, t)\] where:
- \(\mathbf{X}^p(t)\) is the particle position
- \(\tilde{\mathbf{u}}\) is the resolved (filtered) velocity from the LES solver
- \(\mathbf{u}_{SGS}\) represents subgrid-scale velocity fluctuations (modeled)
This represents the physical space component of the full FDF framework, providing immediate applications while establishing the infrastructure needed for composition space transport.
Why Build This Way?
Immediate Applications: While working toward FDF capabilities, the current implementation enables:
- Particle-laden flow simulations: Tracking passive or inertial particles in turbulent flows
- Biomarker transport: Platelet tracking in cardiovascular flows (LVAD studies, thrombosis analysis)
- Pollutant dispersion: Environmental and atmospheric transport problems
- Mixing analysis: Lagrangian diagnostics of turbulent mixing
Technical Foundation: The current phase validates critical infrastructure:
- Parallel particle distribution and load balancing
- Efficient particle-grid interpolation on curvilinear meshes
- Communication patterns for distributed particle ensembles
- I/O frameworks for massive particle datasets
- Integration with CURVIB immersed boundary framework
Risk Mitigation: By establishing particle tracking first, we can:
- Debug spatial transport algorithms independently of composition space complexity
- Validate parallelization strategies with simpler test cases
- Optimize performance bottlenecks before adding stochastic chemistry
- Build confidence in the numerical framework through comparison with analytical solutions
Roadmap to Full FDF
The development follows a staged approach:
Phase 1: Particle Tracking ✅ (Current)
- Newtonian particles following resolved + SGS flow
- Parallel implementation on curvilinear grids
- Applications: particle-laden flows, biomarker tracking
Phase 2: Scalar FDF 🔄 (Next)
- Add composition space transport (Langevin equation for scalars)
- Implement mixing models (IEM, EMST)
- Include chemical source terms
- Validate against DNS data for passive and reacting scalars
Phase 3: Velocity-Scalar FDF (VFDF) ⏭️ (Future)
- Joint velocity-composition PDF transport
- Eliminates SGS stress modeling
- Requires solving for velocity fluctuations at particle locations
Phase 4: Data-Driven Closure ⏭️ (Future)
- Machine learning for SGS convection and mixing
- Physics-informed neural networks
- Training on high-fidelity DNS databases
Building PICurv: Current Implementation & HPC Challenges
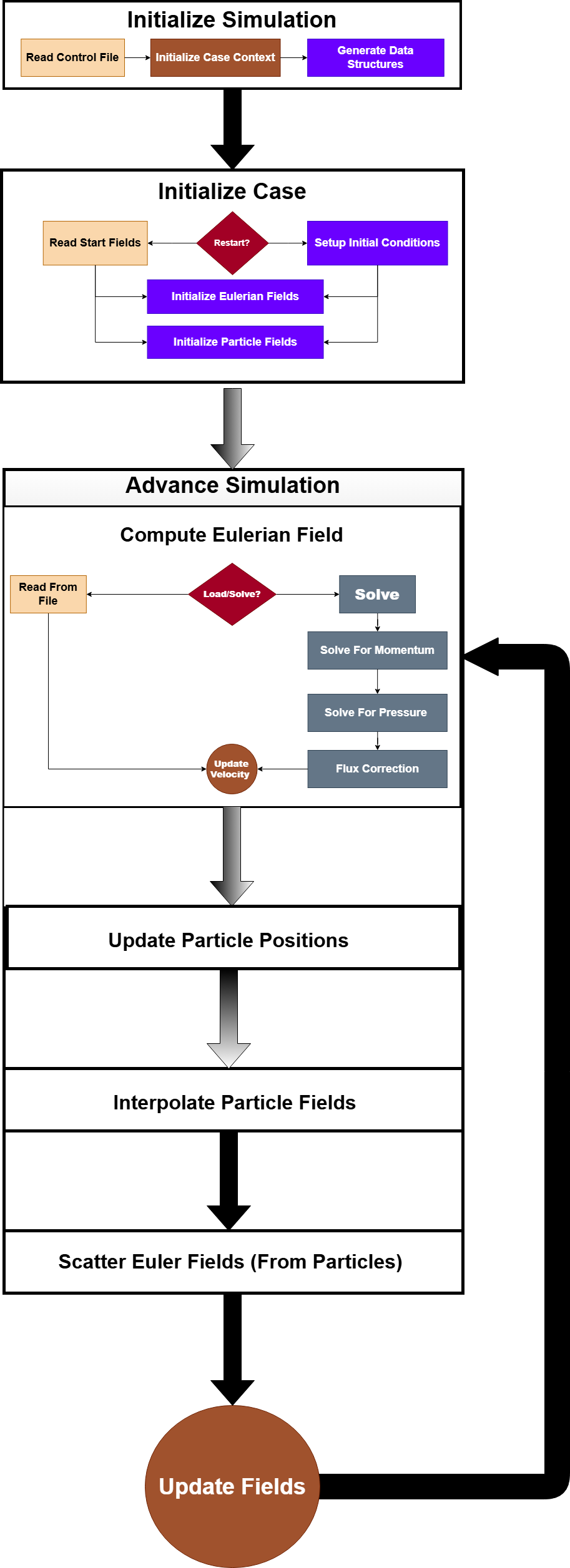
PICurv is being developed as production-quality scientific software with a focus on scalability, maintainability, and extensibility. The current implementation establishes robust Eulerian-Lagrangian coupling for particle transport on curvilinear grids. This foundation will support the eventual FDF framework while providing immediate capabilities for particle-laden flow simulations.
High-level architecture of PICurv showing the modular code organization. The main driver orchestrates the setup phase and time-stepping loop. Each time step involves coupled Eulerian (flow solver) and Lagrangian (particle) updates, operating on shared data structures managed by PETSc.
### Parallel Architecture for Massive Particle Populations The solver is designed from the ground up for distributed-memory parallelism using MPI, targeting simulations with millions to tens of millions of particles across 1000+ compute cores. **DMSwarm Data Structure:** A critical implementation decision is leveraging **PETSc's DMSwarm** (Distributed Memory Swarm) data structure for the Lagrangian component. DMSwarm provides: - Native support for distributed particle ensembles across MPI ranks - Automatic particle migration between ranks as they move through the domain - Efficient parallel I/O for particle data - Integration with PETSc's DM (Distributed Mesh) infrastructure for coupling to Eulerian fields - Built-in particle field management (positions, velocities, scalars) This choice enables tight integration with the existing CURVIB Eulerian solver (which uses PETSc DMDAs for structured grids) while handling the complex logistics of parallel particle management. **Key HPC Challenges:** 1. **Dynamic Load Balancing** - Particles migrate between MPI ranks as they advect through the domain - Maintaining balanced computational load as particle distributions evolve - Efficient particle redistribution strategies with minimal communication overhead 2. **Particle-Grid Communication Patterns** - Particles need access to Eulerian fields (velocity, pressure, SGS quantities) for position updates - Eulerian solver needs particle statistics for filtered quantities - Two-way coupling requires careful orchestration of scatter/gather operations - Minimizing latency and maximizing bandwidth utilization 3. **Memory Management at Scale** - Particle data structures must fit within node memory limits - Dynamic memory allocation/deallocation as particles cross rank boundaries - Efficient storage layouts for cache performance 4. **Scalable I/O** - Parallel output of massive particle datasets for post-processing - Checkpointing strategies for fault tolerance on long-running jobs - Balancing I/O frequency with storage costs ### Integration with CURVIB Framework CURVIB (Curvilinear Immersed Boundary) is an established sharp-interface immersed boundary method for simulating flows around complex geometries on body-fitted curvilinear grids. Integrating particle transport into this framework introduces several technical challenges: **Curvilinear Grid Considerations:** - **Geometric Transformations:** Particle positions must be tracked in both physical and computational coordinates - **Metric Tensor Computations:** Grid stretching and skewness affect interpolation accuracy - **Boundary Treatment:** Particles near immersed boundaries require special handling - **Grid Cell Location:** Efficient algorithms for determining which grid cell contains each particle in non-Cartesian meshes **Data Structure Design:** - Hybrid storage combining structured grid data (Eulerian) with unstructured particle data (Lagrangian) - Efficient spatial indexing for particle-grid queries on curvilinear meshes - Maintaining conservation properties during interpolation/projection operations ### Leveraging PETSc for Linear Algebra The Eulerian LES solver uses PETSc (Portable, Extensible Toolkit for Scientific Computation) for parallel linear algebra operations. This includes: - Krylov subspace methods (GMRES, BiCGStab) for pressure Poisson equation - Preconditioners (ILU, algebraic multigrid) for iterative solvers - Distributed sparse matrix operations - Integration with particle solver requires careful management of PETSc objects and MPI communicators ### Software Engineering Practices Beyond algorithmic development, emphasis is placed on code quality and maintainability: **Code Organization:** - Modular design with clear separation of concerns (particle evolution, field coupling, I/O, etc.) - Object-oriented architecture in C++ for extensibility - Template metaprogramming for performance-critical kernels without sacrificing generality **Documentation & Testing:** - Comprehensive Doxygen documentation for all public interfaces - Inline comments explaining algorithmic choices and implementation details - Automated test suite for regression testing - Unit tests for individual components - Integration tests for coupled Eulerian-Lagrangian system **Development Workflow:** - Version control with Git (GitHub repository) - Continuous integration for automated testing - Performance profiling and optimization workflows - Benchmarking against analytical solutions and reference cases --- ## Parallel Performance Analysis The parallel performance of PICurv has been evaluated through scalability studies on leadership-class HPC systems, focusing on the two most computationally intensive operations in the Eulerian-Lagrangian coupling: 1. **Particle-to-Grid Interpolation:** Transferring Eulerian field values (velocity, pressure) to particle locations 2. **Cell Search/Localization:** Identifying which grid cell contains each particle on curvilinear meshes These operations dominate the computational cost in particle tracking and represent the critical path for overall solver performance.
Preliminary scalability results for (left) grid-to-particle interpolation and (right) particle cell localization on curvilinear grids. Tests performed on [system name] with varying core counts and particle populations. [Image placeholders: Create plots showing parallel efficiency for these specific operations]
**Preliminary Results:** - Interpolation operation shows good parallel efficiency across tested core counts - Cell search algorithm maintains reasonable scalability on body-fitted grids - Communication overhead remains manageable for target particle densities - Both operations demonstrate favorable weak scaling characteristics **Performance Goals:** - Maintain > 80% parallel efficiency for full solver at scale - Support particle populations of 10⁶-10⁷ particles - Target deployment: 1000+ cores for production simulations - Efficient operation on curvilinear/immersed boundary grids **Ongoing Optimization:** - Algorithmic improvements to cell search on complex geometries - Load balancing strategies for spatially non-uniform particle distributions - Communication pattern optimization for DMSwarm migration - Integration of end-to-end solver performance (not just individual operations) **Note:** These are preliminary results from targeted performance tests of specific operations. Full system scalability studies (complete time-stepping with all coupled components) are ongoing as part of dissertation work. --- ## Test Cases & Current Capabilities Current validation focuses on particle tracking in canonical turbulent flows where the Eulerian-Lagrangian coupling can be thoroughly tested against known solutions. ### Fully Developed Turbulent Channel Flow
(Left) Massless tracer particles advecting in fully developed turbulent channel flow at Re=200. Particles are colored by their wall-normal position, demonstrating the solver's ability to track Lagrangian trajectories in turbulent flows. (Right) Particle statistics showing dispersion characteristics. [Image placeholders: GIF showing particle advection, PNG showing particle distributions]
**Configuration:** - Square channel geometry - Reynolds number Re = 200 (based on bulk velocity and channel height) - Massless tracer particles - Periodic boundary conditions in streamwise/spanwise directions - DNS-level resolution (no SGS model at this Re) **Validation Metrics:** - Particle dispersion statistics compared to DNS data - Lagrangian velocity autocorrelations - Particle concentration profiles - Verification of mass conservation in particle ensemble **What this demonstrates:** - Accurate interpolation of Eulerian velocity field to particle locations - Particle tracking through periodic boundaries - Parallel distribution and load balancing - DMSwarm particle migration between MPI ranks **Next Steps:** - Higher Reynolds number simulations (Re > 1000) requiring turbulence models - Implementation of Dynamic Smagorinsky SGS model for LES - Addition of SGS velocity fluctuation models for particle dispersion ### Turbulent Flow in a Bent Channel
(Left) Particle trajectories through 90° bend in square channel at Re=200, colored by velocity magnitude. (Right) Particle dispersion statistics showing effects of secondary flows and pressure gradients. [Image placeholders: GIF of particles through bend, PNG of statistical analysis]
**Configuration:** - 90° square cross-section bend - Reynolds number Re = 200 (based on bulk velocity and channel height) - Massless tracer particles - Tests particle behavior in complex flow regions: - Strong pressure gradients around bend - Secondary flow development (Dean vortices) - Curved boundaries on body-fitted curvilinear grid **Validation Focus:** - Particle dispersion in complex geometry - Conservation in presence of strong gradients - Load balancing as particles migrate through domain - Geometric transformation accuracy on curvilinear coordinates **What this demonstrates:** - Particle tracking on non-Cartesian grids (curvilinear coordinates) - Integration with CURVIB immersed boundary framework - Handling of complex geometries - Parallel efficiency in spatially inhomogeneous flows - DMSwarm cell search performance on body-fitted meshes **Why this test case matters:** The bent channel provides a more realistic test of the infrastructure than simple channel flow: - Non-trivial geometry exercises curvilinear grid capabilities - Spatial flow variations test load balancing algorithms - Strong gradients verify conservation properties - Representative of geometries in biomedical applications (blood vessels, LVAD grafts) ### Current Application: Biomarker Transport Beyond validation cases, the current solver enables immediate scientific applications: **Platelet tracking in cardiovascular devices (LVAD):** - Track individual platelet trajectories through blood pumps - Identify regions of high shear stress (hemolysis risk) - Analyze residence time distributions (thrombosis risk) - Complement Eulerian hemodynamics analysis with Lagrangian diagnostics This work builds on previous LVAD hemodynamics studies (APS DFD 2023) by adding Lagrangian particle tracking capabilities. --- ## Current Status & Development Roadmap **Dissertation Context:** PICurv is being developed as the core contribution of an ongoing Ph.D. dissertation focused on data-driven turbulence closure models. The work follows a staged development strategy, with the current phase focused on establishing robust particle tracking infrastructure. **Current Capabilities (Phase 1):** - ✅ Massless tracer particle tracking in turbulent flows - ✅ Parallel Euler-Lagrange coupling with MPI/PETSc - ✅ Integration with CURVIB framework on curvilinear grids - ✅ Particle-grid interpolation and communication patterns - ✅ Validation test cases: channel flow, bent channel - 🔄 Scalability optimization and performance tuning - 🔄 Application to biomarker transport (platelet tracking in LVAD) **Applications Enabled Now:** - Particle-laden flow simulations (passive tracers, inertial particles) - Biomedical transport problems (platelet tracking, drug delivery) - Lagrangian diagnostics for turbulent mixing - Dispersion analysis in complex geometries **Development Roadmap:** **Phase 2: Scalar FDF Solver** (Next - 2025-2026) - Implement composition space transport (Langevin equation) - Add mixing models: IEM (Interaction by Exchange with the Mean) - Incorporate chemical source terms for reacting flows - Validate against DNS data for passive and reacting scalars - Target: first publication on scalar FDF validation **Phase 3: Velocity-Scalar FDF** (Future - 2026-2027) - Joint velocity-composition PDF transport - Eliminates need for Reynolds stress modeling - Requires solving for velocity fluctuations at particle locations - Complete elimination of traditional SGS modeling assumptions **Phase 4: Data-Driven Closure** (Future - 2027+) - Machine learning for SGS convection and mixing terms - Physics-informed neural networks for closure models - Training/validation using high-fidelity DNS databases - Demonstrate learned closures outperform traditional models - Target: framework for automatic closure discovery **Long-Term Vision:** The ultimate goal is to establish FDF-LES as a practical tool for complex reacting flows, where machine learning algorithms discover optimal turbulence closure strategies directly from high-fidelity simulation data rather than imposing them through modeling assumptions. The current particle tracking framework provides the foundation upon which these advanced capabilities will be built. **Why this matters:** Traditional turbulence modeling requires decades of experience and physical intuition to develop closure models. The FDF+ML approach offers a path to **automatically learn** these closures from data, potentially discovering strategies that human intuition might miss. However, this requires first building the numerical infrastructure to: 1. Track millions of particles efficiently (current phase) 2. Transport scalar PDFs accurately (next phase) 3. Couple with machine learning frameworks (future phase) Each phase builds on the previous, with immediate scientific value while progressing toward the long-term goal. --- ## Resources & Documentation **Code Repository:** - [GitHub: VishalKandala/PICurv](https://github.com/VishalKandala/PICurv) - Open-source release planned upon publication **Documentation:** - [Developer Documentation](https://vishalkandala.me/docs/pic_dev/) - API reference, build instructions, usage examples **Presentations:** - [APS DFD 2025 Houston] - "A Parallel Particle-In-Cell (PIC) Solver on Curvilinear Grids for Turbulent Flow Simulation" (Accepted) - [APS DFD 2023 Washington DC] - "High Resolution Numerical Simulations of LVAD Outflow Graft Haemodynamics" **Contact:** For questions about PICurv or potential collaborations, reach out via [email](mailto:vishalkandala@tamu.edu). ---
Developed in the Scientific Computing and Biofluids Lab at Texas A&M University under the supervision of Dr. Iman Borazjani.